统计学习方法BR-附录:范数
By arthur503 -- 02 Oct 2013
在看统计学习方法的时候,遇到很多数学基础知识的问题,有些概念不知道或不清晰,在这里查下资料备用。
先列一下在查资料之前不了解的问题:在书中会用到||w||来表示w的范数,另外还有区分一阶范数和二阶范数,那分别指的是什么?有没有三阶、四阶范数呢?范数的符号是什么?有几种?它是只有固定的一种算法,还是一类函数的统称?
先看什么是范数。在维基百科中,范数的定义如下:
范数,是具有“长度”概念的函数。在线性代数、泛函分析及相关的数学领域,是一个函数,其为向量空间内的所有向量赋予非零的正长度或大小。半范数反而可以为非零的向量赋予零长度。
唔,看完之后我表示不仅什么都没看懂,反而被一堆名字弄的更迷糊了。我们看他举得一个例子:
举一个简单的例子,一个二维度的欧氏几何空间 R2 就有欧氏范数。在这个向量空间(譬如:(3,7))的元素常常在笛卡儿座标系统被画成一个从原点出发的箭号。每一个向量的欧氏范数就是箭号的长度。
也就是说,一个二维的欧式几何空间中,向量空间中元素的欧式范数就是:在笛卡尔坐标系下,从原点出发到元素的箭头的长度。我们可以理解为是一般意义上的长度。另外,百科中还给出了半范数和范数的定义。半范数有三个条件,范数是半范数+一个额外的条件。不过这几个条件是纯数学式子,看着头晕表示不懂。
之后提到了最常用到的“欧几里得范数”:在n维欧几里德空间 Rn上,向量x = (x1, x2, …, xn)的最符合直觉的长度由以下公式给出: 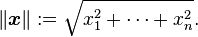
欧几里德范数是Rn上最常用的范数,但正如下面举出的,Rn上也可以定义其他的范数。
在一个n维复数空间Cn中,最常见的范数是: 
在百度百科的解释中,范数的描述多了一句话:范数(norm)是数学中的一种基本概念,在泛函分析中,范数是一种定义在赋范线性空间中函数,满足相应条件后的函数都可以被称为范数。而这里所谓的“相应条件”,就和维基百科里的数学定义一样的了。如果线性空间上定义了范数,则称之为赋范线性空间。
百度百科中,有对范数的分类,包括:算子范数、空间范数和矩阵范数。
算子范数的定义如下:
如果X和Y是巴拿赫空间,T是X->Y的线性算子,那么可以按下述方式定义||T||: ||T|| = sup {||Tx||: ||x|| <= 1} 如果一个性算子T的范数满足||T|| < +∞,那么称T是有界线性算子,否则称T是无界线性算子。
小菜继续表示不懂!
空间范数终于和前面看到的欧几里得范数有点关系了,但是没有定义只有性质。。。尼玛,百度百科不靠谱啊。
常用范数里举例的是p-范数:
若x = [x1, x2, ..., xn],那么: ||x||p = (|x1|p + |x2|p + ... |xn|p)1/p
可以看出,这里的p-范数在p取1、2、∞的时候,分别为绝对值之和、欧几里得距离(即通常意义下的距离)、绝对值中的最大值。
矩阵范数的要求如下:
一般来讲矩阵范数除了正定性,齐次性和三角不等式之外,还规定其必须满足相容性:║XY║≤║X║║Y║。所以矩阵范数通常也称为相容范数。
唔,再次表示看不懂!
在查到的资料中,二范数的百度百科中,有如下定义:
除了矩阵之外,向量和函数均有范数,其中: 矩阵范数:矩阵A的2范数就是 A的转置乘以A矩阵特征根 最大值的开根号; 向量范数:向量x的2范数是x中各个元素平方之和再开根号; 函数范数:函数f(x)的2范数是x在区间(a,b)上f(x)的平方的积分再开根号。
这里的矩阵范数和上面的相同,还是不懂,不过有了矩阵的2范数求值方法;向量的2范数听起来像是之前所说的从原点出发到该元素的向量的长度(也就是原点到改点的欧几里得距离);函数的2范数也不太懂。
查了半天资料,还是不太懂。
不过,在维基百科距离的定义中,有讲到范数如下:
设在Rm空间有两点,p = (p1,p2,...,pm),q = (q1,q2,...,qm),不同的范数都是一种距离: 1-阶范数 = ∑|xi - yi| 2-阶范数 = (∑|xi - yi|2)1/2 n-阶范数 = (∑|xi - yi|n)1/n t 阶范数的极限,即 n 趋向无穷大: 无穷大阶范数 == max|pi - qi|
这就有点清晰了,n阶范数分别为pi和qi差值的n次方,求和后再取1/n次方。在维基百科中范数的定义中,还有一张不同范数的单位元,图片如下: 
我们可以看到,一阶范数为x±y=1的四条线段,二阶范数为单位元,∞阶范数为x=±1和y=±1的四条线段。
最后,我们再来看一下最开始提出的几个问题:
在书中会用到||w||来表示w的范数,另外还有区分一阶范数和二阶范数,那分别指的是什么?有没有三阶、四阶范数呢?范数的符号是什么?有几种?它是只有固定的一种算法,还是一类函数的统称?
根据查到的资料,w可以有p阶(p∈1,∞),他们的范围如上面图中所示。范数的符号就是||w||来表示,可以通过右下角的角标来表示几阶范数。范数的分类有上面提到的矩阵范数、算子范数、空间范数、向量范数(可能有重合的,还需继续理解)等。他是一种定义,满足半范数的条件+一个额外条件即可称为范数。因此,应该是一类函数的统称。至于p-范数等,应该是范数这类里面的一种范数,p-范数有具体的计算定义。
现在的理解就是这样,如果以后有变化了,再来更新吧。
参考资料: