统计学习方法BR-附录：最优化方法、线性规划和非线性规划 test

By arthur503 -- 04 Oct 2013

在查“梯度下降法”的资料的时候，顺便查了下最优化方法，写个概述，作为背景资料备查。

一、最优化方法

1 概念

最优化之前都已经接触过，以前学习的线性规划也是最优化问题的一部分。在维基百科中，最优化方法的描述如下：

最优化（optimization），应用数学的重要研究领域.它是研究在给定约束之下如何寻求某些因素(的量)，以使某一(或某些)指标达到最优的一些学科的总称.由于运筹学中出现的问题大多即是最优化所研究的问题，因此运筹学的许多分支，如数学规划、组合最优化、排队论，以及决策论等也是最优化的组成部分.此外，最优化还包括如工程最优设计、最优控制(控制论与运筹学的交叉分支)等.狭义地说，最优化即指数学规划(参见“数学规划”)，有时也专指非线性规划(参见“非线性规划”).

2 数学定义

准确的说，最优化的数学定义是：

给定一个函数f：A → R，寻找一个元素x⁰ ∈ A，使得对于所有A中的x，f(x⁰) ≤ f(x) (即最小化)；或者f(x⁰) ≥ f(x) (即最大化)

看着意思其实就是寻找整体范围内的最小值或最大值。最优化有时也被称为“数学规划”。在一般意义上，就是我们所理解的求最值，有全局最优解和局部最优解。

3 符号表示

最优化的符号表示为：

min<sub>x∈R</sub> f(x)

这是求函数f(x)的极小值（也可以使用max来转化为求最大值）。或者还可以求取最值时参数x的取值，其符号表示为：

arg min<sub>x∈R</sub> f(x)

4 主要分支

最优化问题的主要分支包括：

线性规划：当目标函数f是线性函数而且集合A是由线性等式函数和线性不等式函数来确定的，我们称这一类问题为线性规划。 * 整数规划：当线性规划问题的部分或所有的变量局限于整数值时，我们称这一类问题为整数规划问题。
二次规划：目标函数是二次函数，而且集合A必须是由线性等式函数和线性不等式函数来确定的。 * 非线性规划：研究的是目标函数或是限制函数中含有非线性函数的问题。 * 非线性规划：研究的是目标函数或是限制函数中含有非线性函数的问题。 * 随机规划：研究的是某些变量是随机变量的问题。 * 动态规划：研究的是最优策略基于将问题分解成若干个较小的子问题的优化问题。 * 组合最优化：研究的是可行解是离散或是可转化为离散的问题。 * 无限维最优化：研究的是可行解的集合是无限维空间的子集的问题，一个无限维空间的例子是函数空间。

从我目前来看，最有用的就是线性规划和非线性规划。上面列表中，整数规划为线性规划的特例（所有变量为整数）；二次规划是非线性规划的特例（目标函数为二次函数）。

5 相应算法

为了解决最优化问题，求解算法列了很多。

对于无约束的优化问题，如果函数是二次可微的话，可以通过找到目标函数梯度为0（也就是鞍点）的那些点来解决此优化问题。

要找到拐点，我们可以通过猜测一个初始点，然后用比如以下的迭代的方法来找到。迭代方法包括：

* 梯度下降法 * 牛顿法 * 共轭梯度法 * 线性搜索 * 置信域方法

也就是说，我之前在查的“梯度下降法”是最优化方法的算法中，迭代方法的一种。

另外，如果目标函数在我们所关心的区域中是凸函数的话，那么任何局部最小解也是全局最优解。现在已经有稳定，快速的数值计算方法来求二次可微地凸函数的最小值。

有约束条件的约束问题常常可以通过拉格朗日乘数转化为非约束问题。

其他流行方法还包括：

* 模拟退火 * 遗传算法 * 类免疫算法 * 演化策略 * 差异演化算法 * 微粒群算法 * 神经网络 * 支持向量机

下面我们对最优化方法中的两个分支，“线性规划”和“非线性规划”研究一下。

二、线性规划

1 概念

线性规划在高中的数学书中就有所涉及，当时主要用的方法是对划出各条线，得到取值范围（也就是可行域），然后利用目标函数的直线进行平移，直到与可行域接触，得到最优解。

现在再重新来看一下说明，在维基百科中,线性规划的描述为：

在数学中，线性规划 (Linear Programming，简称LP) 问题是目标函数和约束条件都是线性的最优化问题。

线性规划是最优化问题中的重要领域之一。很多运筹学中的实际问题都可以用线性规划来表述。线性规划的某些特殊情况，例如网络流、多商品流量等问题，都被认为非常重要，并有大量对其算法的专门研究。很多其他种类的最优化问题算法都可以分拆成线性规划子问题，然后求得解。在历史上，由线性规划引申出的很多概念，启发了最优化理论的核心概念，诸如“对偶”、“分解”、“凸性”的重要性及其一般化等。同样的，在微观经济学和商业管理领域，线性规划被大量应用于解决收入极大化或生产过程的成本极小化之类的问题。乔治·丹齐格被认为是线性规划之父。

2 数学描述

线性规划有三种形式，最常用的（也就是之前提到过的）是标准型，例如：1.一个需要极大化的线性函数；2.非线性不等式形式的问题约束；3.非负变量。

其他还有增广矩阵形式，引入非负松弛变量将不等式约束变成等式约束；还有对偶形式，如把最大化问题转化为最小化问题。

3 理论

集合上，线性约束条件的集合相当于一个凸包或凸集，也就是可行域。一般情况下，线性目标函数的最优解在可行域的顶点中取得，最优解未必唯一，可以是一组最优解。

有两种例外情况，是没有最优解的。

1. 约束条件互相矛盾，可行域为空，无解，所以也没有最优解。 2. 约束条件的多面体可以在目标函数的方向上无界，这样目标函数可以取任意大的值，因此没有最优解。

4 算法

求解线性规划的算法有好几种，前面提到的属于单纯形算法，其他还有椭球法、内点算法，以及投影尺度法等，具体用到的时候再查看。

5 特例：整数规划

整数规划是线性规划的特例，对其描述如下：

要求所有的未知量都为整数的线性规划问题叫做整数规划 (integer programming, IP) 或整数线性规划 (integer linear programming, ILP) 问题。相对于即使在最坏情况下也能有效率地解出的线性规划问题，整数规划问题的最坏情况是不确定的，在某些实际情况中（有约束变量的那些）为NP困难问题。

三、非线性规划

1 概念

在维基百科中，非线性规划的描述如下：

非线性规划问题是利用非线性规划研究一个n元实函数的极值问题，且目标函数和约束条件至少有一个是未知量的非线性函数。

也就是说，非线性规划是研究在目标函数和约束条件中，至少有一个未知量为非线性函数的极值问题。

2 数学描述

非线性规划的数学表达式描述如下：

min<sub>x∈X</sub> f(x)

受限条件是：

g(x) ≤ 0
h(x) = 0

其中：

f: R<sup>n</sup> → R
X 包含于 R<sup>n</sup>

定义域X中满足约束条件的点称为问题的可行解(注：与线性规划中的可行域相对应)。

与线性规划相比，非线性规划还没有适用于各种问题的一般算法，各种算法都有自己特定的适用范围。唔，竟然是还没有通用解法，还是有待学习啊。

最后，附上思维导图：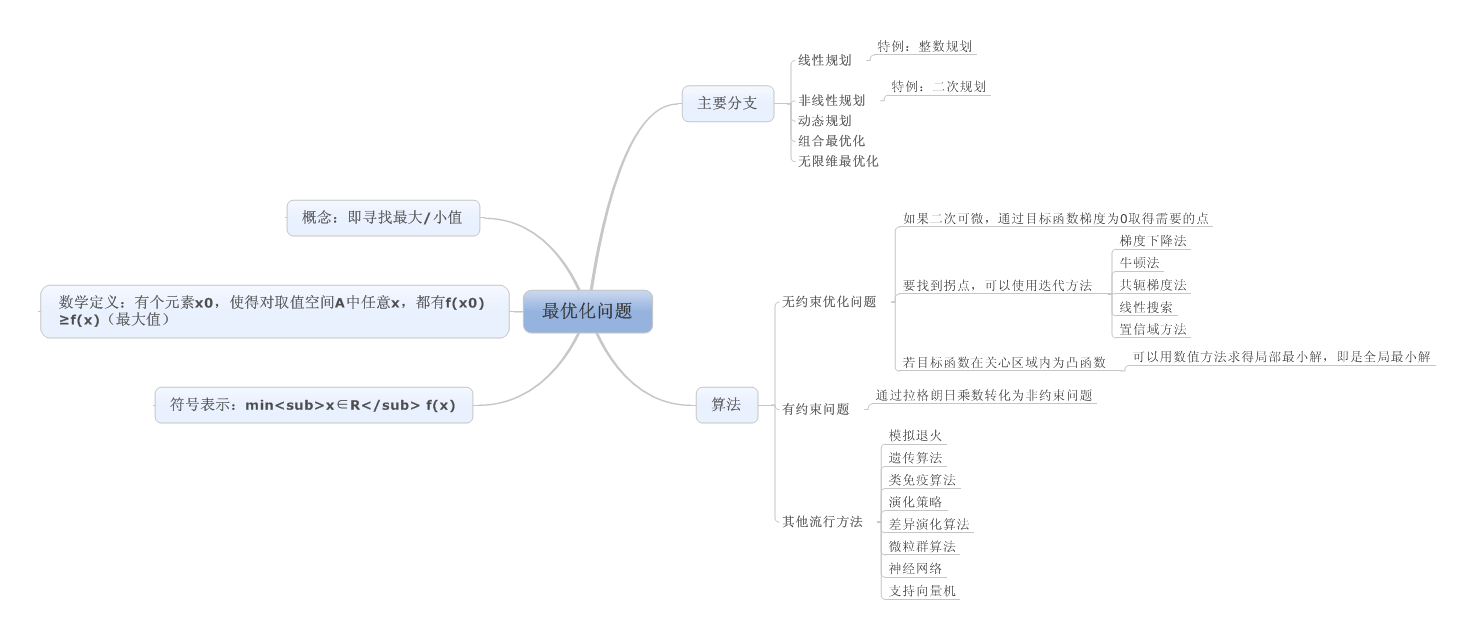

参考资料：