机器学习CR-EP02：监督学习应用与梯度下降【待补充代码实现】

EP02中主要讲了线性回归(Linear Regression)、梯度下降(Gradient Descent)、正规方程组(Normal Equation)。

先举了个线性回归的应用的例子，是15年前与CMU合作的自动汽车驾驶项目。现在自动汽车驾驶技术蓬勃发展，Google也在做实验，估计离商业化也不远了的样子，不过在15年前，还是很牛逼的。自动汽车驾驶系统叫做Alvin，使用的核心算法就是Gradient Descent和神经网络。训练的步骤为：

真人驾驶，Alvin学习。每两秒自动拍摄前方道路并记录驾驶员方向盘操作（左转右转等），拍摄的图像转化为30 * 30像素的图像，作为三层神经网络的输入。随着训练的进行，2min之后Alvin预测的方向盘操作和驾驶员的实际操作已经基本一致了。 2. 在不同的道路上进行训练。
切换到Alvin驾驶。可以看到，在单行道上，Alvin的驾驶不错，置信度confidence也很高。不过，中间有一处路过十字路口，道路有交叉，而且路面颜色也不一致，Alvin在通过的时候预测有些混乱，confidence也骤减。不过还是顺利通过，通过之后confidence也回升到正常情况。

看完这个例子的video之后，回到房价预测的例子上来。这是一个线性回归的典型应用场景。根据房间的面积、卧室面积等来预测房子的价格。是要训练一个线性回归模型。

基本的机器学习的模型如下图所示：

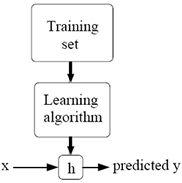
其中，h表示hypothesis function，也就是假设函数。

在房价预测的例子中，假设函数最后可以归为：

J(θ) = frac{1}{2}∑_{i=1}^{n}(h_{θ}(x^{(i)})-y^{(i)})^{2}
min J(θ)

最终的结果化为J(θ)函数的最小化。

计算J(θ)函数最小化的方法有几种：

算法思想为：先设定初始θ向量（如0^{→}）；之后迭代更新，逐步减小J(θ)函数，直至J(θ)函数收敛。中间迭代更新，可以理解为寻找下山的最快路径（寻找梯度的反方向）。

这里有个问题是：如何判断收敛？可以看两次更新迭代中的值是否改变很多；更常用的是检验J(θ)的值，即：需要最小化的值若不再经常改变，则称为收敛。

不过，通过推导之后的结果，算法中每次计算0^{i}，都需要遍历m个数据元素。那么，n个特征就需要遍历mn次。对每个数据元素都需要计算n个特征，因此总的时间复杂度是O(m^2 * n)。因此，批梯度下降法在大数据集的时候，效率比较低。因此，在数据量比较大的时候，我们使用下一种方法。

随机/增量梯度下降法的计算中，每次更新0的值的时候，不再遍历m个元素数据，而是只是用这一次的元素，因此，可以将时间复杂度降低到O(mn)，大大加快计算速度。不过，这样的后果是不会精确的收敛到全局最小值，可能只在全局的最小值附近迂回徘徊。

3. 批梯度下降法的快速计算

Andrew在课堂上利用线性代数的方法，进行一系列符号推导，最后得到：

X^{T}X0 = X^{T}y

这就是Normal Equation。可以推得：

0 = (X^{T}X)^{-1}X^{T}y

这样，可以进行对梯度进行快速计算，从而加快计算速度。

【待补充】